根号三约等于多少，根号三等于多少

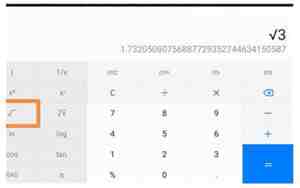
根号三，通常用数学符号表示为√3，是一个无理数，其值精确到小数点后很多位是1.7321。但因为它是一个无限不循环的小数，我们通常在实际计算中会取近似值。在日常教学和简单计算中，通常用约等于1.73，但如果你需要更高的精度，可以使用计算器得到更准确的结果。例如，四舍五入到两位小数就是1.73，如果需要更多位数，可以自行计算或查询。

根号三怎么算

根号三（√3）的计算通常没有简单的代数形式，因为它是无理数，不能被写成两个整数的比。无理数是指不能简单表示为两个整数比的数，比如圆周率π和根号三。

不过，有一种常见的估算方法。如果你需要一个近似值，可以使用长除法或者计算器。一个常见的方法是使用泰勒级数或者马赫林公式来展开根号三，但对于一般的教育或日常计算，我们可以使用以下步骤：

1. 用分数近似法：√3 ≈ 1 + 1/2 - 1/8 + 1/16 - 1/32 + ...，这是1的平方根的无限序列，每个分母都是2的幂。

2. 用小数表示：√3 ≈ 1.7320508075688772，这是计算器给出的近似值。

记住，这些方法可以帮助你快速得到一个合理近似，对于精确值，除非是计算专业人士，否则一般不会手动进行复杂的无限级数展开。

根号三是什么意思

根号三（√3）是数学中的一个表达式，它代表3的平方根，即求一个数3的非负平方根。想象一下，如果有一个数乘以它自己等于3，那么这个数就是根号三。实际上，根号三是一个无理数，不能被表示为两个整数的乘积，其小数部分是无限不循环的，大约等于1.7321（四舍五入到四位小数）。根号三在几何中也有重要应用，例如在等边三角形的计算中，它的边长、对角线长度和高都有直接的关系。