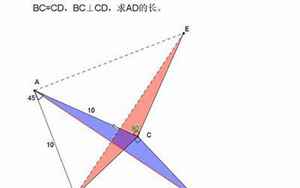
截长补短法(平面几何辅助线专题之三角形全等之截长补短法)

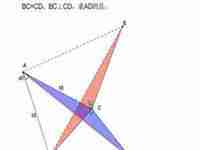
截长补短法，作为一个重要的平面几何辅助线方法，可以帮助我们解决很多几何问题。在三角形全等问题中，截长补短法也起到了至关重要的作用。

首先，我们需要了解三角形全等的定义。两个三角形全等，意味着它们的三边和三角度量都相等。根据这个定义，我们可以知道，在三角形全等问题中，需要找到至少三个相等的量才能得到答案。

接下来，让我们来介绍一下截长补短法在三角形全等问题中的应用。

1. 三角形边边边全等。

在三角形ABC和DEF中，若AB=DE，BC=EF，AC=DF，则三角形ABC和DEF全等。

这个定理是三角形全等中最简单的一种情况。我们可以通过截长补短法来证明它。

我们在三角形ABC和DEF中，分别连接AC和DF。由于AC=DF，我们可以在AC和DF上分别取一个相等的线段AD和CF，使得AD=CF。这样，我们就将三角形ABC和DEF都分成了两个小三角形。

由于AD=CF，我们可以得到三角形ABD和DEF、三角形CBD和EFC都是全等的。因此，有AD+DB=CF+EB，即AB+BD=DE+EF，即AB+BC+CA=DE+EF+FD。因此，根据边边边全等的定义，我们可以得到三角形ABC和DEF全等。

2. 三角形边角边全等。

在三角形ABC和DEF中，若AB=DE，∠A=∠D，BC=EF，则三角形ABC和DEF全等。

这种情况下，我们可以通过截长补短法来证明三角形ABC和DEF全等。

我们在三角形ABC和DEF中，分别连接AC和DF。我们再分别在AB和DE上截取线段AE和DB，使得AE=BD，连接CE和FB。

由于∠A=∠D，我们可以在AE和DB上分别作角平分线AF和DC，它们会在点K上相交。

由于AE=BD，我们又可以知道∠KAF=∠KDC。因此，我们可以得到三角形AKF和DCK都是全等的。因此，有AK=DC。又因为∠AKC和∠DFB都是直角，因此可以得到AK和DC分别是∠A和∠D的高。因此，我们可以得到∠BAC=∠EDF。

由于AB=DE，我们又可以知道∠ABD和∠DEA都是直角。因此，我们可以得到三角形ABD和DEA都是全等的。因此，有BD=AE。

因此，我们可以得到AB+BC=DE+EF且∠BAC=∠EDF且AB=DE。因此，根据边角边全等的定义，我们可以得到三角形ABC和DEF全等。

3. 三角形角边角全等。

在三角形ABC和DEF中，若∠A=∠D，AB=DE，∠B=∠E，则三角形ABC和DEF全等。

这种情况下，我们同样可以通过截长补短法来证明三角形ABC和DEF全等。

我们在三角形ABC和DEF中，分别连接AC和DF。我们再在AB和DE上分别截取线段AE和DB，使得AE=BD。我们再连接CE和FB。

由于∠A=∠D，我们可以得到三角形ABD和DEA都是全等的。因此，有BD=AE。

我们在三角形ABC和DEF中，分别作三角形的高AJ和DK。因为∠A=∠D，我们可以得到AJ=DK。又因为∠B=∠E，我们可以得到BJ=EK。

因此，我们可以得到∠BAC=∠EDF、AB=DE且BJ=EK。因此，根据角边角全等的定义，我们可以得到三角形ABC和DEF全等。

通过上面三种情况的证明，我们可以得到一个结论：在三角形全等问题中，截长补短法是一个非常有用的辅助线方法，它可以帮助我们找到三个相等的量，从而得到答案。同时，我们也需要注意，截长补短法的应用需要灵活，需要结合具体的问题来选择适当的辅助线。

截长补短法的8种方法

截长补短法是指在阅读或写作时，针对文本中长短不一的不足或缺陷进行有针对性地切割和补充，以提高文本质量和可读性的方法。以下是截长补短法的8种方法：。1. 省略冗长的词语或句子，从而使文本更加简洁明了。2. 添加具体的细节和描写，以便更加生动形象地表达观点和体现情感。3. 合并重复的内容或表达方式，以避免重复和冗余，从而增加文本的紧凑性。4. 将过于抽象或无法理解的概念或词汇转化为更具体和易于理解的语言，以提高读者的理解和接受度。5. 改变文本的结构，使其更加有条理和连贯，以方便读者阅读和理解。6. 加强逻辑性和连贯性，使文本的各个部分之间具有更加紧密和清晰的联系，以提高文本的整体一致性和逻辑性。7. 重新组织文本的段落和章节，以增强文本的层次感和分明度，从而使读者更容易理解和接受。8. 利用图片、图表、表格等辅助工具来展示信息和数据，以提高文本的可视化程度和直观性。

初中几何证明方法之截长补短法

截长补短法是初中几何证明方法之一，它常用于证明几何图形的形状和大小。具体方法如下：。1. 首先，根据题目所给条件画出几何图形，并标明各个已知条件。2. 然后，从图形中找出可以截取或补充的线段或图形，使得该线段或图形与已知条件能够形成一个新的几何关系。3. 接着，根据新的几何关系和已知条件，运用已学过的几何定理或公式进行计算，最终得出所求结论。例如，我们要证明一个三角形的角度和为180度。首先，我们画出一个三角形ABC，并标明其三个内角α、β、γ。然后，我们在三角形的一条边AB上取一点D，连接CD。由三角形内角和定理可知：三角形ABC的三个内角之和等于180度，即α+β+γ=180度。我们将三角形ABC分成两个三角形：三角形ABD和三角形BCD。根据三角形内角和定理可知：三角形ABD的内角之和等于180度，即α+β+∠ADB=180度。又根据三角形内角和定理可知：三角形BCD的内角之和等于180度，即β+γ+∠CDB=180度。将以上两式相加，得到：。α+2β+γ+∠ADB+∠CDB=360度。由于∠ADB+∠CDB=180度（三角形ABD和三角形BCD共线），因此上式可简化为：。α+β+γ=180度。因此，三角形ABC的角度和为180度，得证。

截长补短法处理线段和差问题

截长补短法是一种用于处理线段和差问题的技巧。其主要思想是将一个线段拆分成两个部分，分别进行计算，再将结果合并起来。如果需要计算两个线段的和差，可以考虑截长补短，将较长的线段拆分成两个短线段，再分别与另一个线段进行计算。例如，设线段AB和线段CD的长度分别为a和c，则可以将线段AB拆分成线段AE和线段EB，其中AE的长度为c，EB的长度为a-c。然后，可以计算AE与CD的和差，以及EB与CD的和差，最后将结果合并起来即可得到线段AB和线段CD的和差。如果需要计算一个线段的平方和或差，也可以使用截长补短法。例如，设线段AB的长度为a，则可以将它拆分成线段AE和线段EB，其中AE的长度为a-1，EB的长度为1。然后，可以计算AE的平方和与EB的平方和，以及AE与EB的和差，最后将结果合并起来即可得到线段AB的平方和或差。截长补短法可以使计算更加简单明了，特别适用于处理复杂的线性运算问题。