对数函数公式大全(对数运算的公式是什么)

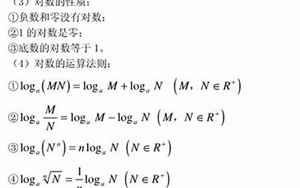
对数函数是数学中一个非常重要的概念，被广泛应用于各个领域。在数学中，对数函数可以用来解决各种复杂的问题，因此学习对数函数及其公式对于提高数学能力至关重要。本文将介绍对数函数的基本概念和常用公式，帮助读者了解对数函数及其应用。

一、对数函数的基本概念。

对数函数是指一个以底数为基数的指数函数，其定义域为正实数集，值域为实数集。对数函数的定义式为：y=loga(x)，其中a为底数，x为真数，y为对数。

对数函数的形式特别简洁，但它的意义却非常深刻。在实际应用中，对数函数可以将复杂的计算问题转化为更简单的形式，方便人们进行理解和计算。例如，在工程学、物理学、经济学等领域中，对数函数可以用来描述各种现象和规律，被广泛应用于实际问题中。

二、对数函数的基本性质。

在数学中，对数函数具有以下几个基本性质。

1.对数函数的定义域为正实数集，值域为实数集。

2.以任何正实数为底数的对数函数在定义域内是一一对应的。

3.以不同底数的对数函数之间可以相互转化。

4.对数函数的反函数为指数函数。

5.对数函数具有单调增加性质。

6.对数函数满足对数加法公式、对数减法公式、对数乘法公式、对数除法公式和对数换底公式。

三、对数函数的常用公式。

1.对数加法公式。

对数加法公式是对数函数中比较基础的一个公式，其公式表达式为：。

loga(x*y)=loga(x)+loga(y)。

其中，a为底数，x、y为非零正实数。对数加法公式可以简化乘法运算，将乘法运算转化为加法运算，方便进行计算和推导。

2.对数减法公式。

对数减法公式是对数函数中比较基础的一个公式，其公式表达式为：。

loga(x/y)=loga(x)-loga(y)。

其中，a为底数，x、y为非零正实数。对数减法公式可以简化除法运算，将除法运算转化为减法运算，方便进行计算和推导。

3.对数乘法公式。

对数乘法公式是对数函数中比较基础的一个公式，其公式表达式为：。

loga(x^n)=n*loga(x)。

其中，a为底数，x为非零正实数，n为任意实数。对数乘法公式可以简化乘方运算，将乘方运算转化为乘法运算，方便进行计算和推导。

4.对数除法公式。

对数除法公式是对数函数中比较基础的一个公式，其公式表达式为：。

loga(x^n/y^m)=n*loga(x)-m*loga(y)。

其中，a为底数，x、y为非零正实数，n、m为任意实数。对数除法公式可以简化带分数的计算，将带分数运算转化为对数运算，方便进行计算和推导。

5.对数换底公式。

对数换底公式是对数函数中比较重要的一个公式，其公式表达式为：。

loga(b)=logc(b)/logc(a)。

其中，a、b、c为三个不同的正数。对数换底公式可以将不同底数的对数函数进行转化，以便于进行计算和推导。

四、结语。

对数函数及其公式是数学学科中非常重要的一个部分，对于提高数学能力和解决实际问题具有非常重要的意义。本文介绍了对数函数的基本概念和常用公式，希望能够帮助读者更好地理解对数函数及其应用。同时，我们也希望读者能够继续深入学习数学知识，不断提高自己的数学能力。

对数函数的一些基本运算公式

1. 常用对数函数公式：。$log_{10}x=y$，其中$x$为实数，$y$为以10为底的对数，等价于$x=10^y$。2. 自然对数函数公式：。$lnx=y$，其中$x$为实数，$y$为以自然数$e$为底的对数，等价于$x=e^y$。3. 对数函数的乘法公式：。$log_ab+log_ac=log_a(bc)$，其中$a>0$，$a\neq1$，$b>0$，$c>0$。4. 对数函数的除法公式：。$log_ab-log_ac=log_a(\frac{b}{c})$，其中$a>0$，$a\neq1$，$b>0$，$c>0$。5. 对数函数的幂公式：。$log_ab^n=n\cdot log_ab$，其中$a>0$，$a\neq1$，$b>0$，$n$为实数。6. 对数函数的换底公式：。$log_ab=\frac{log_cb}{log_ca}$，其中$a>0$，$a\neq1$，$b>0$，$c>0$，$c\neq1$。换底公式可以将一个对数转化为另一个底数的对数，有助于简化计算。7. 对数函数的指数公式：。$a^{log_ab}=b$，其中$a>0$，$a\neq1$，$b>0$。对数函数的指数公式可以将指数、底数和对数相互转化。

对数公式全部合集

1. logab = loga + logb。2. loga/b = loga – logb。3. loga^n = n loga。4. logab^n = n logab = n (loga + logb)。5. loga√x = (1/2)loga x。6. loga x = logb x / logb a。7. loga x = 1 / logx a。8. ln(ex) = x。9. elnx = x。10. loga 1 = 0。11. loga a = 1。12. log1 x = 0。13. loga(ax) = x。14. loga x = loga b * logb x。15. loga x + loga y = loga (xy)。16. loga x – loga y = loga (x/y)。17. loga x^n = n loga x。18. loga (x + y) ≠ loga x + loga y (only works for multiplication and division)。19. loga ∞ = ∞。20. loga 0 = Undefined (for a > 0)。

对数函数的十个公式是什么呢

对数函数公式大全：。1. log(ab) = log(a) + log(b) -- 对数的乘法法则。2. log(a/b) = log(a) - log(b) -- 对数的除法法则。3. log(a^n) = n*log(a) -- 对数的指数法则。4. log(1) = 0 -- 对数的基本性质。5. log(a) = log(b) => a=b -- 对数的反函数性质。6. ln(e) = 1 -- 自然对数底数e的对数等于1。7. log(a^m)/log(a^n) = m/n -- 转化不同底数的对数。8. loga(b) = logc(b) / logc(a) -- 转化不同底数的对数。9. loga(1/x) = -loga(x) -- 对数的倒数法则。10. loga√n = 1/2loga(n) -- 对数的平方根法则。这十个公式是对数函数的基本法则，其中前三个法则是最为常用的。

很全的对数函数的公式推导

1. 对数函数定义：loga(x)，其中a为底数，x为真数。2. 换底公式：loga(x) = logb(x) / logb(a)，其中b为任意底数。3. 对数运算法则：。(1)loga(xy) = loga(x) + loga(y)。(2)loga(x/y) = loga(x) - loga(y)。(3)loga(x^n) = nloga(x)。(4)loga(1/x) = -loga(x)。(5)loga(x) = logb(x) / logb(a)。(6)loga(e) = 1/ln(a)。4. 对数函数的导数：。(1)d/dx (loga(x)) = 1 / (xln(a))。(2)d/dx (alog(x)) = (a/x)。(3)d/dx (a^x) = (a^x)ln(a)。5. 对数函数的积分：。(1)∫ 1/x dx = ln|x| + c。(2)∫ a^xdx = (a^x) / ln(a) + c。(3)∫ loga(x) dx = xloga(x) - x + c。6. 对数函数的常见性质：。(1)对数函数的值域为实数集。(2)对数函数是单调递增的。(3)对数函数的反函数是指数函数。(4)当底数a>1时，对数函数呈现上凸弧形状；当底数0