平行四边形的面积教案，平行四边形的面积教案免费

【解锁几何秘密：平行四边形面积公式探索之旅】

【一、导入新课】

大家好，今天我们要一起走进几何世界，探索平行四边形面积的奥秘！你是否想象过，一个简单的矩形或菱形，只要知道一边的长度和另一边的倾斜角度，就能计算出它能覆盖多大地面？这就是我们今天要解密的——平行四边形面积。孩子们，准备好你的笔记本和，我们这就出发！

【二、概念解析】

让我们明确一下平行四边形。它是一种有两对平行边的四边形，想想你课桌的桌面，或者学校的足球场，它们就可能是平行四边形的原型。平行四边形的特点是边对边平行，这将帮助我们计算面积。

【三、公式揭秘】

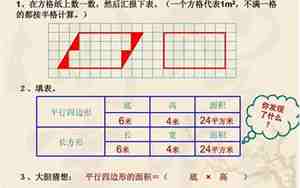
关键的时刻来了，平行四边形的面积公式是什么呢？它就是底乘以高，用专业术语表达就是：\( A = \text{底} \times \text{高} \)。这里的"底"就是任意一对平行边中较短的一边，"高"则是垂直于底的边的长度。简单来说，就像把平行四边形划分成无数个小小的矩形，然后加起来的总面积。

【四、实例计算】

现在，让我们通过一个实际例子来理解和应用这个公式。假设我们有一个平行四边形，底边长为12厘米，高为8厘米。那么，面积\( A = 12\ \text{cm} \times 8\ \text{cm} = 96\ \text{cm}^2 \)。是不是觉得简单又神奇呢？

【五、拓展应用】

我们学了公式，但知识的真正价值在于应用。想象一下，如果建筑师需要设计一块草坪，或者园艺师要在这个面积上铺瓷砖，他们就能利用这个公式轻松计算所需材料的数量。几何知识，生活中无处不在！

【六、课堂练习】

现在，是时候检验你们的理解了。请你们在练习本上完成几道题目，比如一个底边长为5米、高为3米的平行四边形面积是多少？别忘了，实践出真知！

【七、课堂小结】

通过今天的课程，我们不仅学习了平行四边形的面积公式，还通过实例和练习巩固了知识。记住，数学是一门工具，理解和运用它，能让我们更好地解释世界。那么，下一次你看到商铺的招牌、草地的修剪，或者家里的床单，都可以尝试用这个公式来估算它的面积哦！

祝大家在探索几何世界的过程中，充满乐趣，学以致用！下课！

平行四边形的面积教案北师大版

【北师大版平行四边形面积教案：快乐发现几何的秘密】

【一、导入新课】

同学们，上节课我们学习了三角形和梯形，今天我们将继续探索更有趣的几何图形——平行四边形。想象一下你的美术工具箱，里面的平行尺子就是三角形和平行四边形的完美结合。今天，我们要解开平行四边形面积的神秘面纱！

【二、概念回顾】

先回顾一下，平行四边形的定义是什么？它有两对平行边，这对我们的面积计算有着特殊的意义。今天我们将学习如何利用这个特点来计算面积。

【三、新知讲解】

好，我们要揭开的神秘公式是：平行四边形的面积\( A \)等于底乘以高。这里的"底"是平行四边形任意一边的长度，高的定义是与底垂直的线段长度。想象一下，这个平行四边形就像是一块长方形，只不过对边是平行的。

【四、实例演示】

让我们通过一个实例来阐明这个道理。如果一个平行四边形的底是15厘米，高是10厘米，面积\( A \)就是\( 15 \text{cm} \times 10 \text{cm} = 150 \text{cm}^2 \)。是不是觉得简便又神奇呢？

【五、互动活动】

现在，老师给你们每人准备了一张平行四边形纸片，试着用尺子找出底和高，和同桌一起计算面积，看看你们合作得如何！

【六、公式应用】

让我们回到生活中的场景，比如家里的窗台、学校的操场，这些都可以看作平行四边形。通过面积公式，我们可以计算需要多少草皮或者壁纸来覆盖这些区域。

【七、课堂练习】

完成作业：计算一个底为8米，高为6米的平行四边形的面积。记住，公式已经在你们心中生根发芽了！

【八、小结与延伸】

今天的课程，我们不仅学习了平行四边形的面积计算，还学会了如何把它运用到实际问题中。记住，数学不仅是理论，更是生活的一部分。在日常生活中，时刻留意身边的几何形状，用所学知识去解决问题，你就是生活中的小小几何学家！

【作业布置】
1. 画出并计算一个实际场景中的平行四边形面积（例如桌布、花园等）。
2. 尝试自己设计一个题目，考验同学们对平行四边形面积公式的理解。

下一个课时，我们将继续探索更复杂的几何图形，敬请期待！下课！

平行四边形的面积教案设计意图

平行四边形的面积教案设计意图主要包括以下几个方面：

1. 知识传授： 通过具体的讲解和实例，让学生理解平行四边形面积的计算公式，这是几何基础知识的重要组成部分，为后续学习其他图形面积打下基础。

2. 技能培养： 通过动手操作和课堂练习，引导学生进行实际操作，提高他们运用公式解决问题的能力，培养他们的计算能力。

3. 思维训练： 让学生思考生活中的平行四边形，如课本、窗户、田地等，这有助于培养他们的空间观念和实际应用能力。

4. 合作学习： 互动活动和与同桌的合作，旨在培养学生的团队协作，提高他们的沟通和解决问题的能力。

5. 情感教育： 通过有趣的数学情境，激发学生对数学的兴趣，让他们体验到数学在生活中的实用性，从而增强学习的主动性和自信心。

6. 目标导向： 教案设计的目标明确，比如掌握平行四边形面积的计算，能够在实际问题中应用，这有助于老师评估学生的学习进度。

7. 实践操作： 通过实际操作，让学生体验数学知识的实践性，这有助于他们把理论知识转化为实际技能，培养动手能力。

8. 评价与反馈： 教案设计中包含课堂反馈和作业布置，能够及时了解学生的掌握情况，进行针对性的指导。

平行四边形面积教案设计旨在全面发展学生的数学技能，提升他们的数学素养，同时鼓励他们探索和应用数学知识，体验学习的乐趣。