四边形的内角和是多少度，三角形的内角和是多少度

四边形的内角和是360度。无论四边形的形状如何，比如正方形、长方形、梯形或者不规则四边形，其内部所有角度的和总是固定的，等于360度。这是由于每个顶点处的两个内角和相邻的两个内角共同组成一个180度的直角，所以四个顶点相加即是360度。

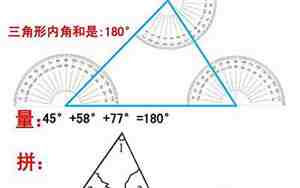
三角形的内角和是180度。这是因为在任意三角形中，三个内角的和总是等于180度。这是因为三角形的任意两边之和大于第三边，所以三个角度相加会形成一个不小于180度的总和。这是几何学中的基本定理，适用于所有类型的三角形，包括直角三角形、锐角三角形和钝角三角形。

三角形的斜边怎么求公式

在直角三角形中，斜边（也称为对边或Hypotenuse）的长度可以用勾股定理来计算。勾股定理是描述直角三角形三条边（两直角边和斜边）之间关系的公式，它表明：

\[ c^2 = a^2 + b^2 \]

其中：
\( c \) 是斜边的长度，
\( a \) 和 \( b \) 是直角边的长度。

如果你想求斜边，你可以将其中一边的长度平方，然后加上另一边的平方，然后开平方根得到斜边的长度。如果已知两边的长度，应用公式如下：

\[ c = \sqrt{a^2 + b^2} \]

如果只知道一个边和它的对角，再加上已知角度，可以使用反正切（arctangent，记作 \( \tan^{-1} \) 或 \( \arctan \)）来计算斜边，因为在一个直角三角形中，正切值等于对边长度除以邻边长度，如果角度是锐角：

\[ c = b \cdot \tan(\theta) \]

或者对于角度 \( \theta \)：

\[ c = a \cdot \frac{1}{\tan(\theta)} = a \cdot \cot(\theta) \]

这里 \( b \) 或 \( a \) 是已知边的长度，\( \theta \) 是对应的锐角。

六边形的内角和怎么算

六边形的内角和可以通过一个简单的公式计算，这个公式基于多边形内角和的一般规则。对于任意多边形（n边形），其内角和 \( S \) 可以用以下公式计算：

\[ S = (n - 2) \times 180^\circ \]

其中 \( n \) 是多边形的边数。所以，对于六边形（n=6），内角和 \( S \) 可以这样计算：

\[ S = (6 - 2) \times 180^\circ = 4 \times 180^\circ = 720^\circ \]

因此，六边形的内角和是720度。这个角度是通过将180度分配到每个内角，然后乘以6边的数量来得到的。因为每个内角与相邻的两个内角加起来总是180度，所以总和除以边数就是每个内角的平均度数。