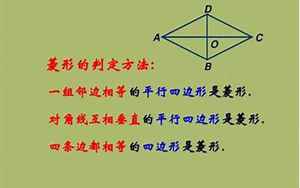
菱形判定(菱形的判定条件)

菱形判定是一种几何学中常用的方法，用于判断一个四边形是否为菱形。菱形的判定条件是其四条边相等，且对角线相互垂直。

菱形是一种特殊的四边形，具有独特的性质和特征。因为它的四条边相等，所以每个角也都相等，为90度。同时，菱形的对角线互相垂直，并且相互平分。这些性质使得菱形在几何学中具有重要作用，在建筑学、机械工程等领域也得到广泛应用。

那么，如何判定一个四边形是否为菱形呢？菱形判定有以下几种方法：。

1. 观察四边是否相等。菱形的四条边必须全部相等，才能满足菱形的定义。如果一个四边形的四条边不相等，那么它就不可能是菱形。

2. 观察对角线是否相等。菱形的对角线必须相等，才能满足菱形的定义。如果一个四边形的对角线不相等，那么它就不能是菱形。

3. 观察对角线是否相互垂直。菱形的对角线必须相互垂直，也就是说，它们的夹角必须为90度。如果一个四边形的对角线不垂直，那么它就不能是菱形。

4. 使用勾股定理判断对角线是否相互垂直。勾股定理是指：直角三角形的两条直角边的平方和等于斜边的平方。如果我们已知一个四边形的所有边长，可以使用勾股定理来判断它的对角线是否相互垂直。首先求出对角线的长度，然后使用勾股定理判断它们是否相互垂直。

5. 使用角平分线定理判断对角线是否相互垂直。角平分线定理是指：一个三角形的内角平分线相互垂直，且交点离对边的距离等于相邻边长之比的积乘以对边长。如果我们已知一个四边形的所有边长，可以使用角平分线定理来判断它的对角线是否相互垂直。

需要注意的是，以上五种判定方法并没有必须使用全部的限制条件。例如，只需要观察四边是否相等和对角线是否相等就可以判断一个四边形是否为菱形。使用多种方法进行判断可以更加准确地确定一个四边形是否为菱形。

总之，菱形是一种常见的四边形，具有重要的几何性质和特征。菱形判定可以通过多种方法进行，判断一个四边形是否为菱形，有助于对几何学的学习和理解。

菱形的判定方法4条合集

菱形判定是指判断一个四边形是否为菱形。以下是4条菱形判定方法的合集：。1. 对角线相等定理：如果一个四边形的两条对角线相等，则这个四边形是菱形。2. 对边角相等定理：如果一个四边形的对面两个角相等，则这个四边形是菱形。3. 对边平行定理：如果一个四边形的对边两两平行，则这个四边形是菱形。4. 对边垂直定理：如果一个四边形的对边互相垂直，则这个四边形是菱形。以上4条规律可以互相验证，如果一个四边形符合其中任意一条规律，则它就是菱形。

菱形的判定方法

菱形是一个四边形，它的四条边长相等，且对角线相交于90度角。判定方法：。1. 判断四条边是否相等，如果不相等则不是菱形。2. 判断对角线是否相等，如果不相等则不是菱形。3. 判断对角线是否垂直，如果不垂直则不是菱形。4. 如果四边相等且对角线相等并垂直，则是菱形。5. 可以通过计算四个角的大小是否相等来判断是否为菱形，因为菱形的四个角大小都为90度。

菱形的证明定理合集

菱形判定定理：。在平面直角坐标系中，对于点 $A(x_1,y_1)$，$B(x_2,y_2)$，$C(x_3,y_3)$，$D(x_4,y_4)$，如果满足以下条件之一，则四边形 $ABCD$ 是菱形：。1.四个点两两距离相等：$AB=BC=CD=DA$。2.对角线互相垂直且交于中点：$AC$ 垂直于 $BD$ 且 $AC$ 的中点与 $BD$ 的中点重合，即 $\overrightarrow{AC}\cdot\overrightarrow{BD}=0$ 且 $\frac{\overrightarrow{AC}}{2}=\frac{\overrightarrow{BD}}{2}$。3.对角线长度相等：$AC=BD$。菱形的证明定理：。1.四个点两两距离相等：。证明：根据勾股定理，设 $AB=a$，$BC=b$，$CD=c$，$DA=d$，则有：。$(x_2-x_1)^2+(y_2-y_1)^2=a^2$。$(x_3-x_2)^2+(y_3-y_2)^2=b^2$。$(x_4-x_3)^2+(y_4-y_3)^2=c^2$。$(x_1-x_4)^2+(y_1-y_4)^2=d^2$。将其整理成矩阵形式：。$$。\begin{pmatrix}。2(x_2-x_1)&2(y_2-y_1)&-2(x_4-x_3)&-2(y_4-y_3)\\。-2(x_2-x_1)&-2(y_2-y_1)&2(x_3-x_2)&2(y_3-y_2)\\。0&0&2(x_4-x_3)&2(y_4-y_3)\\。0&0&-2(x_1-x_4)&-2(y_1-y_4)。\end{pmatrix}。\begin{pmatrix}。a^2\\。b^2\\。c^2\\。d^2。\end{pmatrix}。=。\begin{pmatrix}。0\\。0\\。0\\。0。\end{pmatrix}。$$。由于四个点不共线，所以上述矩阵的行列式不为 $0$，因此其秩为 $4$，即只有零解，所以四边形 $ABCD$ 是菱形。2.对角线互相垂直且交于中点：。证明：设 $\overrightarrow{AB}=\langle x_2-x_1,y_2-y_1\rangle$，$\overrightarrow{BC}=\langle x_3-x_2,y_3-y_2\rangle$，$\overrightarrow{CD。