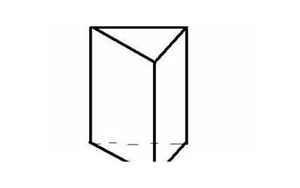
正三棱柱的特点(正三棱柱有什么特点)

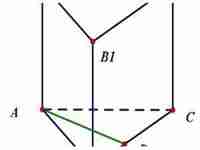
正三棱柱是一种几何体，它具有很多特点和特征。在本篇文章中，我将详细讲解正三棱柱的特点，以帮助读者更好地了解这种几何体。

首先，正三棱柱是由六个等边三角形组成的几何体。这意味着正三棱柱的六个面都是等边三角形，每个角度都是60度。由于这个特点，正三棱柱的所有边长和角度都相等，因此非常规则。

其次，正三棱柱具有对称性。正三棱柱有三个轴对称，分别是沿着柱子的长轴，以及沿着柱子两端的轴对称。这意味着正三棱柱可以通过旋转来重叠，因为它们具有相同的形状和大小。

再次，正三棱柱的体积可以通过使用公式V = Bh来计算，其中B是正三角形的面积，h是正三棱柱的高度。因为正三角形的面积可以通过应用公式A = (sqrt(3)/4)*a²来计算，其中a是正三角形的边长，所以正三棱柱的体积公式可以简化为V = (sqrt(3)/4)*a²*h，使计算变得更为容易。

此外，正三棱柱的表面积可以通过使用公式S = 2B + Ph，其中B是正三角形的面积，P是正三角形的周长，h是正三棱柱的高度。因为正三角形的周长可以通过应用公式P = 3a来计算，所以正三棱柱的表面积公式可以进一步简化为S = (3sqrt(3)/2)*a² + 3ah。

最后，与其他几何体一样，正三棱柱还有一些重要的性质。例如，正三棱柱的对角线长度可以通过应用公式D = a*sqrt(3)来计算，其中a是正三角形的边长。此外，正三棱柱的所有棱和面的角度都是相等的。

总之，正三棱柱是一种非常规则的几何体，具有许多特点和性质。它由六个等边三角形组成，每个角度都是60度，具有对称性且易于计算其体积和表面积。因此，正三棱柱是几何学中一个非常重要的形状，可以在许多实际应用中发挥作用。

正三棱柱的性质

正三棱柱是一个有六个面的多面体，它的特点是：。1. 正三棱柱的底面是一个正三角形，顶部也是一个正三角形；。2. 正三棱柱的侧面是三个相等的矩形；。3. 正三棱柱的底面中心和顶部中心之间的距离等于侧面的长度。正三棱柱的性质包括：。1. 正三棱柱的底面积为（3/4）×a²×√3，其中a为正三角形的边长；。2. 正三棱柱的侧面积为3a×h，其中h为正三棱柱的高度；。3. 正三棱柱的表面积为（3+3√3）×a²；。4. 正三棱柱的体积为（1/3）×a²×h；。5. 正三棱柱是一个轴对称图形，它有三个轴对称线：分别是从底面的每个顶点到对面的顶点的轴对称线。正三棱柱具有对称美和稳定性，广泛应用于建筑、设计和艺术领域。