抛物线的准线方程(的准线方程是)

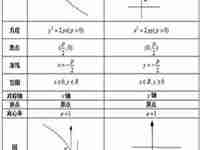
抛物线是一种常见的数学曲线，其特点是形如二次函数的方程，定点称为焦点，定直线称为准线。在抛物线的研究中，准线方程是非常重要的一个概念，本文将以抛物线的准线方程为主题，详细介绍它的定义、性质以及实际应用。

一、准线方程的定义。

定义抛物线的焦点为点F，准线为直线L，过焦点F的直线与准线L的交点为点P，抛物线上任意一点Q到焦点F的距离与点Q到准线L的距离之差为常数。这个常数称为抛物线的离心率e。则准线方程可以表示为：。

y = ± e x。

其中，x是任意实数，y是对应的准线上的点的纵坐标。

二、准线方程的性质。

1. 准线方程的对称性：抛物线关于准线对称，即对于任意一点(x,y)，其对称点为(x,-y)。

2. 准线方程的导数：准线方程的导数是常数e，即：。

y’ = ± e。

其中，y’是准线方程的导数。

3. 准线方程的切点：准线方程上的任意一点都是抛物线的切点。

4. 准线方程与焦准距的关系：焦点F到准线L的距离为焦准距，任意一点P到准线L的距离为点准距，则焦准距的平方等于点准距的平方加上常数e的平方。

5. 准线方程与抛物线的离心率的关系：离心率e等于焦准距除以抛物线的顶点到焦点F的距离。

三、准线方程的实际应用。

1. 数学解题的应用：当我们需要求解抛物线上任意一点到准线的距离时，可以通过准线方程来计算。

2. 物理学中的应用：抛物线常常用来描述物体的运动轨迹。在飞行器的设计中，我们需要知道飞行器的抛物线轨迹与准线的关系，以便预测飞行器在不同高度下的运动状态。

3. 工程设计中的应用：在桥梁设计中，我们需要考虑抛物线的准线方程来确定桥梁的弧形，以使得桥梁的承重能力得到最大的提升。

综上所述，抛物线的准线方程是抛物线研究中不可或缺的一个概念，通过准线方程可以计算抛物线上各点到准线的距离、求解焦准距等问题。此外，准线方程还具有对称性、导数和切点等重要性质，其在数学、物理和工程等领域中都具有重要的应用价值。

题目和参考答案

题目：求抛物线 $y=ax^2+bx+c$ 的准线方程。参考答案：抛物线的准线方程为 $y=c-\dfrac{b^2}{4a}$。