拐点和驻点的区别(什么是驻点和拐点)

在数学中，驻点和拐点是两个常见的概念。它们在函数的图像中有重要的意义，可以帮助我们更好地理解函数的变化和特性。

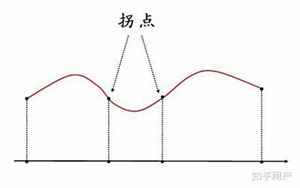
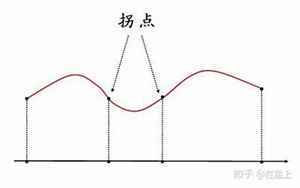
首先，让我们来看看驻点和拐点的定义。驻点是指函数的导数为零的点，也就是函数图像上出现的平稳点。在这个点附近，函数的变化趋势将会发生变化。拐点则是指函数图像上出现的拐弯点，在这个点处，函数的曲线将会发生变化，由凹向上变为凹向下或者由凹向下变为凹向上。拐点处的导数为零，但是它相邻的两个导数的符号是不同的。

驻点和拐点在函数的图像中有很重要的意义。当我们在观察一个函数的图像时，我们可以利用驻点和拐点来帮助我们确定函数的变化趋势。例如，在一个函数的图像中，当我们发现一个驻点时，我们可以判断函数在这个点附近的变化趋势。如果这个点右侧的导数是正数，左侧的导数是负数，那么这个驻点就是一个函数的局部极大值。反之，如果这个点右侧的导数是负数，左侧的导数是正数，那么这个驻点就是一个函数的局部极小值。

类似地，当我们在一个函数的图像中发现一个拐点时，我们可以利用它来判断函数的凹凸性。例如，如果一个函数在某个区间上是凹向上的，而在另一个区间上是凹向下的，那么这两个区间之间的拐点就是函数的拐点。这个点将会把函数的凹凸性从凹向上变为凹向下，或者从凹向下变为凹向上。

除了在观察函数的图像时，驻点和拐点也有很多其他的应用。例如，在优化问题中，我们可以利用驻点来求函数的最大值和最小值。在微积分中，我们可以利用拐点来求函数的弧长和曲率半径。

总之，驻点和拐点是数学中常见的概念，它们在函数的图像中有重要的意义，可以帮助我们更好地理解函数的变化和特性。在学习数学时，我们应该重视这些概念，灵活运用它们，提高我们的数学素养。

驻点与拐点区别

拐点和驻点都是函数图像的特殊点。拐点指的是函数曲线的转折点，其处导数发生突变。在拐点处，函数的二阶导数为零或不存在。而驻点指的是函数的极值点，其处导数为零。在驻点处，函数的二阶导数可为零、正数或负数。因此，拐点和驻点的区别在于是否存在导数的突变。驻点既可以是函数的最大值点，也可以是最小值点，相比之下拐点只是函数曲线的转折点。

驻点与拐点的区别

拐点和驻点都是函数图像上的特殊点。拐点是指函数图像上的一个点，该点处的曲率发生突变或变化的方向发生变化。在拐点处，函数的导数仍然存在。驻点是指函数图像上的一个点，该点处的斜率为零。在驻点处，函数的导数等于零。因此，拐点和驻点的区别在于，拐点是曲线变化方向的点，而驻点是斜率为零的点。此外，驻点处可以是函数的最大值、最小值或拐点，但拐点不一定是驻点。