拐点怎么求(方法步骤是什么)

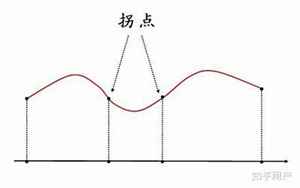
拐点在数学中也被称为转折点，它是函数曲线上的一个点，在这个点处曲线的切线斜率发生了变化。求拐点的方法有多种，以下将介绍其中几种常用的方法。

一、一阶导数和二阶导数法。

这是较为常用的方法。我们先对函数进行一次求导，再对求导后的结果再次求导，从而得到函数的二阶导数。二阶导数为零的点即为拐点。

例如，对于一个函数 $f(x)$，我们先求其一次导数：。

$$。

f'(x)=\frac{df(x)}{dx}。

$$。

再对一次导数 $f'(x)$ 求导：。

$$。

f''(x)=\frac{d^2f(x)}{dx^2}。

$$。

当 $f''(x)=0$ 时，$x$ 就是拐点所在位置。

二、曲率半径法。

曲率是曲线的弯曲程度，曲率半径就是曲率的倒数。在 $f(x)$ 的点 $x_0$ 处，曲率半径的计算公式如下：。

$$。

R(x_0)=\frac{[1+(f'(x_0))^2]^{\frac{3}{2}}}{f''(x_0)}。

$$。

拐点处的曲率半径为无穷大，因为拐点的曲率为零。因此，当 $f''(x_0)=0$ 时，$x_0$ 为拐点。

三、三阶导数法。

这种方法需要对函数进行三次求导，因此较为繁琐。我们先求得函数的三阶导数：。

$$。

f'''(x)=\frac{d^3f(x)}{dx^3}。

$$。

当 $f''(x)=0$ 时，$x$ 是可能的拐点所在位置。接着，我们求 $f'''(x)$ 在 $x$ 处的值，若 $f'''(x)\neq0$，则 $x$ 不是拐点。若 $f'''(x)=0$，则 $x$ 是拐点。

总而言之，以上三种方法都可以求出函数的拐点，其具体使用范围依据个人选择而定。同时，需要注意，在使用这些方法时，我们对函数的定义域和区间也要进行分析，以保证求出的拐点符合实际需求。

判断拐点的简单方法

拐点的求法：。1. 求出函数的导数，即找到函数变化率的变化率，即二阶导数。2. 利用二阶导数的符号来判断拐点的存在与否：。- 若二阶导数大于0，则函数呈现上凸形状，不存在拐点；。- 若二阶导数小于0，则函数呈现下凸形状，不存在拐点；。- 若二阶导数等于0，则可能存在拐点，需要进一步判断。3. 当二阶导数发生符号的变化时，就存在拐点。判断拐点的简单方法：。1. 如果函数图像呈现出上凸形状，则不存在拐点。2. 如果函数图像呈现出下凸形状，则不存在拐点。3. 如果函数图像呈现出“V”字形，则存在一个拐点。4. 如果函数图像呈现出“W”字形，则存在两个拐点。

函数的拐点怎么求

函数的拐点是指函数图像上出现转折的点，也就是函数的二阶导数为零的点。求函数的拐点需要以下步骤：。1. 求函数的一阶导数。2. 求函数的二阶导数。3. 解二阶导数为零的方程，得到函数的拐点坐标。具体来讲，假设函数为$f(x)$，则可以按照以下步骤求拐点：。1. 求$f(x)$的一阶导数$f'(x)$。2. 求$f'(x)$的二阶导数$f''(x)$。3. 解方程$f''(x)=0$，得到$x$的值。4. 将$x$值带入$f(x)$，求出对应的$y$值，得到拐点的坐标。需要注意的是，函数的拐点不一定存在，其存在的条件为函数存在二阶导数且二阶导数在拐点附近发生了变号。

拐点是怎么求的

拐点是函数图像上的极值点，即函数在这个点上由上升转为下降或由下降转为上升，因此求拐点的方法是找出函数的导数，然后求出导数的零点，即找到函数的极值点，然后在极值点的两侧计算二阶导数，如果二阶导数为正，说明函数在该点处具有局部最小值，是一个上凸拐点；如果二阶导数为负，说明函数在该点处具有局部最大值，是一个下凸拐点。如果二阶导数为零，说明该点可能是拐点，需要进一步分析。

求函数拐点的一般步骤

求函数的拐点，需要求出它的二阶导函数。一般步骤如下：。1. 求函数的一阶导数（即导函数）；。2. 求导函数的导数（即二阶导函数）；。3. 解二阶导函数的零点，得到函数的拐点横坐标；。4. 将拐点横坐标代入原函数，求出拐点纵坐标。具体求解过程可以参考下面的例子：。例题：求函数 $y=3x^4-4x^3$ 的拐点。解：首先求一阶导数：。$$y'=12x^3-12x^2$$。再求二阶导数：。$$y''=36x^2-24x$$。解方程 $y''=0$，求得 $x=0$ 或 $x=\dfrac{2}{3}$。于是函数 $y=3x^4-4x^3$ 的拐点横坐标为 $x=0$ 和 $x=\dfrac{2}{3}$。将 $x=0$ 和 $x=\dfrac{2}{3}$ 代入原函数，得到拐点的纵坐标：。$$y(0)=0,\quad y\left(\dfrac{2}{3}\right)=\dfrac{16}{27}$$。所以函数 $y=3x^4-4x^3$ 的两个拐点分别为 $(0,0)$ 和 $\left(\dfrac{2}{3},\dfrac{16}{27}\right)$。