初三数学黄金分割公式(黄金分割计算公式是什么)

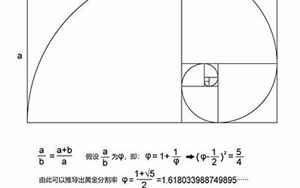
黄金分割公式是数学中的一种重要公式，也称为黄金比例公式。该公式经常被用于艺术、建筑、音乐和金融等领域，被认为是一种美学上的标准。黄金分割公式的应用广泛，最常见的是用于计算黄金分割点。

黄金分割点是指将一段线段分成两个部分，使得其中一部分长度与整段长度之比等于另一部分长度与这一部分之比。黄金分割点的比例为1:0.618033988749895。这个比例可以用黄金分割公式来计算。

黄金分割公式是这样的：设一个线段的长度为a，将这个线段分成两个部分，其中一部分的长度为x，另一部分的长度为a-x。如果x与a-x的比例等于a与x的比例，那么x与a-x的长度比就是黄金分割点的比例。用公式表示为：。

x/a = a/(a-x)。

解这个方程可以得到：。

x = a*(√5-1)/2。

a-x = a- a*(√5-1)/2 = a*(1-√5)/2。

这就是黄金分割点的比例公式。

黄金分割点的比例不仅出现在数学中，还在艺术、建筑和自然界中广泛应用。例如，在音乐中，黄金分割点的比例可以用来确定音乐的节奏和节拍。在建筑中，黄金分割点的比例可以用来设计建筑物的比例和比例尺寸，使得建筑物具有更加和谐的美学感受。在自然界中，黄金分割点的比例可以用来描述一些事物的大小和形状，如花朵、树木、人脸等。

黄金分割点的比例不仅在美学上有用，还在金融和投资中广泛应用。例如，在股票和商品交易中，黄金分割点的比例可以用来确定价格波动的重要趋势线和支撑线。在技术分析中，黄金分割点的比例可以用来预测价格的变化和做出买卖决策。

总之，黄金分割点的比例是一种重要的美学和数学基础，具有广泛的应用价值。无论是在艺术、建筑、音乐、自然界还是金融和投资中，黄金分割点的比例都是一种有用的工具，可以帮助我们更好地理解事物的大小、比例和结构。

黄金分割率的十个公式

黄金分割公式：。1. 黄金分割点公式：$\frac{a}{b}=\frac{b}{a-b}$。2. 黄金分割比公式：$\frac{1+\sqrt{5}}{2}=1.61803398875$。3. 黄金分割数列公式：$F_n=F_{n-1}+F_{n-2}$，其中$F_0=0$，$F_1=1$。4. 黄金长方形公式：长和宽之比为黄金分割比，面积为$a^2$。5. 黄金三角形公式：一边长为黄金分割数，角度为$36^\circ$，其余两个角度为$72^\circ$。6. 黄金比例线段分割公式：$AC:CB=1:\phi$，其中$\phi$为黄金分割比。7. 黄金比例垂线分割公式：$AE:ED=\phi:1$，其中$\phi$为黄金分割比。8. 黄金比例面积分割公式：$S_1:S_2=\phi:1$，其中$\phi$为黄金分割比。9. 黄金比例体积分割公式：$V_1:V_2=\phi^2:1$，其中$\phi$为黄金分割比。10. 黄金比例线段分割二次公式：$AB:BC=1:(1+\sqrt{5})/2$，其中$\sqrt{5}$为黄金分割比的平方。

黄金分割比例是几比几

黄金分割比例是1:1.618，即前一部分与后一部分的比例为1:1.618。黄金分割公式是：。A/B = B/(A+B)。其中A为整体，B为被分割出来的较小部分，A+B为剩余部分。