众数怎么求(中位数怎么求)

众数和中位数是统计学中较为常见的概念，它们可以帮助我们更好地了解数据的特征和分布。

一、众数的求法。

众数是指在一组数据中出现次数最多的数值，也就是数据的“最常见值”。在实际问题中，我们常常需要找出一组数据中的众数，以便进一步分析研究。

求众数的方法主要有以下几种：。

1.直接统计法。

直接统计法是最简单、最直接的求众数的方法。具体步骤如下：。

（1）将一组数据按照大小顺序排列；。

（2）统计每个数值出现的次数；。

（3）找出出现次数最多的数值，即为众数。

例如，对于以下一组数据：2，4，3，2，1，2，3，2，5，6，2，4。

我们可以按照上述步骤进行计算，得到每个数值出现的次数如下：。

1出现1次，2出现5次，3出现2次，4出现2次，5出现1次，6出现1次。

因此，这组数据的众数为2。

2.分组统计法。

如果一组数据的范围比较大，那么直接统计法的效率可能会比较低。此时可以采用分组统计法，将一组数据按照一定的范围划分成若干组，然后统计每组中出现次数最多的数值，最终得到这组数据的众数。

例如，对于以下一组数据：10，11，12，13，14，15，16，17，18，19，20，21，22，23，24，25，26，27，28，29，30。

我们可以将这组数据以每5个数据一组的方式进行划分，得到如下分组：。

10~14，15~19，20~24，25~30。

然后统计每个组中出现次数最多的数值，最终得到这组数据的众数为20。

3.数形结合法。

数形结合法是一种比较直观、易于理解的求众数的方法。具体步骤如下：。

（1）将一组数据按照大小顺序排列；。

（2）将数据用图形表示出来（如直方图或条形图）；。

（3）找出图形中最高的那个柱子对应的数值，即为众数。

例如，对于以下一组数据：5，4，6，2，3，5，7，6，2，8，4，6。

我们可以将这组数据用直方图表示出来，如下图所示：。

[这里插入图片]。

从图中可以看出，最高的那个柱子对应的数值为6，因此这组数据的众数为6。

二、中位数的求法。

中位数是指一组数据中“中间”的那个数值，也就是将所有数值按照大小顺序排列后，处于中间位置的数值。如果这组数据的数量为偶数，那么中位数就是中间两个数值的平均值。

求中位数的方法主要有以下几种：。

1.直接排序法。

直接排序法是最常用的求中位数的方法。具体步骤如下：。

（1）将一组数据按照大小顺序排列；。

（2）如果数据的数量为奇数，那么中位数就是排序后位于中间位置的数值；。

（3）如果数据的数量为偶数，那么中位数就是排序后中间两个数值的平均值。

例如，对于以下一组数据：3，4，1，5，6，2。

我们可以按照上述步骤进行计算，先将数据排序如下：。

1，2，3，4，5，6。

然后找出中间位置的数值，即中位数。由于这组数据的数量为偶数，因此中位数为中间两个数值的平均值，即（3+4）/2=3.5。

2.差值法。

差值法是一种比较简单、适用范围广的求中位数的方法。具体步骤如下：。

（1）将一组数据按照大小顺序排列；。

（2）计算出数据的最大值和最小值；。

（3）用最大值减去最小值，得到一个差值；。

（4）将这个差值除以2，得到一个中位数的偏移量；。

（5）用最小值加上这个偏移量，就得到了中位数。

例如，对于以下一组数据：7，4，9，2，5，8。

我们可以按照上述步骤进行计算，先将数据排序如下：。

2，4，5，7，8，9。

然后计算出最大值和最小值，分别为2和9。将其相减得到一个差值7，然后除以2得到中位数的偏移量3.5。最后用最小值2加上偏移量3.5，得到中位数为5.5。

求众数的公式

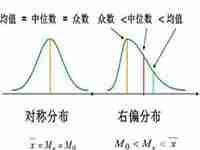
众数是一组数据中出现次数最多的数，可以通过以下公式进行求解：。1. 对于不重复的数据集，众数等于出现次数最多的数。2. 对于有重复数据的数据集，可以使用频数分布表或直方图来找到众数。3. 可以通过计算数据集的中位数、平均数和众数之间的差异来判断数据的分布形态。如果众数等于中位数和平均数，表明数据集呈现正态分布。如果众数小于中位数和平均数，表明数据集呈现左偏态分布。如果众数大于中位数和平均数，表明数据集呈现右偏态分布。例如，以下数据集中出现次数最多的数为5，则5为该数据集的众数。2, 4, 5, 3, 5, 6, 5, 7, 1, 5。