二阶导数大于0说明什么(请问二阶导大于0的凹凸性)

二阶导数大于0说明了函数的凹性。这个结论可以帮助我们了解函数图像的特征以及函数的变化趋势。

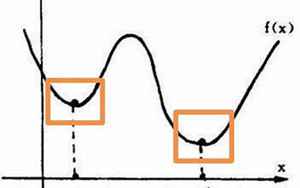
首先，我们需要知道什么是二阶导数。我们已经知道导数描述了函数$f(x)$在$x$处的变化率。二阶导数是对一阶导数的导数。如果我们用$f'(x)$表示$f(x)$的导数，那么$f''(x)$就是$f'(x)$的导数。换言之，二阶导数描述了$f(x)$的变化率的变化率。如果$f''(x)>0$，那么$f'(x)$将逐渐变大。这意味着$f(x)$将会在$x$处凸起。

凸函数通常具有以下性质：。

1. 函数的图像总是向上凸起；。

2. 从左往右看，函数的斜率逐渐变大；。

3. 函数上的所有点都位于函数的下方；。

4. 函数在$x$处的曲率比在$x-1$处的曲率更大。

这些性质可以帮助我们更好地了解函数的行为。例如，如果我们知道一个函数$f(x)$的二阶导数是正的，我们可以确定它是一个凸函数，而不必绘制函数的图像。我们还可以确定函数的拐点，因为拐点是函数从凸到凹的位置。在拐点之前，函数凸起；在拐点之后，函数凹陷。

当然，这并不是说函数的所有部分都是凸的。函数可能会在某个点上发生凹陷。在这些点附近，二阶导数将变为零或负值。如果$f''(x)<0$，那么$f(x)$在$x$处凹陷。凹函数通常具有以下性质：。

1. 函数的图像总是向下凹陷；。

2. 从左往右看，函数的斜率逐渐变小；。

3. 函数上的所有点都位于函数的上方；。

4. 函数在$x$处的曲率比在$x+1$处的曲率更小。

凹函数与凸函数形成鲜明的对比。它们在图像中形成了“山谷”，而凸函数形成的是“山峰”。凹函数的拐点是函数从凹到凸的位置。在拐点之前，函数凹陷；在拐点之后，函数凸起。

二阶导数大于0的凸性简直重要。它使我们能够准确地描述函数的特征，如拐点和凸凹性。它也使我们能够更好地理解和掌握微积分的基础概念。因此，我们应该尽可能多地了解这个主题，以便更好地掌握微积分。

函数二阶导数大于零是什么意思

二阶导数大于0表示函数的曲率变大，即曲线呈现出向上凸的形状。在数学上，当函数的二阶导数大于0时，表示函数的斜率增加，即函数的变化速率在增大。这通常意味着函数的增长速度在加快，或者函数的下降速度在减缓。函数二阶导数大于零通常被视为函数具有正的凸性，即函数曲线向上弯曲。