中位数的概念(中位数是什么意思)

中位数是数学中的一个概念，是指一组数据中位于中间位置的数值。在统计学中，中位数是一组数据中分布中间点的度量，通常用于描述一组数据的集中趋势。

中位数是按照大小排列后位于中间位置的数值。如果数据有奇数个，中位数就是中间那个数；如果数据有偶数个，那么中位数就是中间两个数的平均值。例如，假设有一组数据为2，3，5，7和9，这组数据中位数就是5。而如果这组数据为2，3，5，6，7和9，中位数就是(5+6)/2=5.5。

中位数是一组数据中的一个重要度量，与平均值相比，它更能够反映数据的分布情况。例如，假设有一个班级的成绩分别为50，60，70，80，90，如果这个班级的平均分为70分，那么我们会认为这个班级的成绩还不错。但是如果我们知道这个班级的成绩分数分别为10，20，70，80，90，那么这个班级的平均分还是70分，但是实际上，这个班级的成绩分布情况非常不均，大部分的学生成绩很低。因此，这个时候我们应该使用中位数来描述这个班级的成绩情况，中位数为75分，反映了这个班级的成绩大部分集中在中等水平以上。

另外，在一些特殊情况下，中位数的应用也非常广泛。例如，在贷款领域，人们经常使用收入的中位数来衡量一个家庭的财务状况。在政府公共政策制定中，政策制定者也经常使用中位数来衡量整个国家或地区的经济发展水平。在医学领域，中位数也被用来判断疗效的好坏。

在实际应用中，计算中位数也很简单。例如，假设有一个样本集合S={x1,x2,…,xn}，那么中位数的计算方法如下：。

1. 将样本集合按照大小排列。

2. 如果样本集合的大小为奇数，那么中位数就是排列后位于中间位置的那个数。

3. 如果样本集合的大小为偶数，那么中位数就是排列后中间两个数的平均值。

总之，中位数作为一种常用的统计学指标，具有较强的可比性和普遍性，可以在各个领域中发挥重要的作用。在实际应用中，我们应该根据具体情况选择合适的指标来描述数据的分布情况，以便更好地进行分析和决策。

中位数的意义

中位数是指一组数据按照大小排序，中间位置的数值，如果数据个数是奇数，则中位数就是这组数据中间位置的数值；如果数据个数是偶数，中位数则是中间两个数的平均值。中位数的意义在于其具有普遍性和稳定性。相对于平均数，中位数更能反映一组数据的中间位置，不容易被极端数据的影响而产生偏差。因此，中位数在统计分析中被广泛应用，例如在人口、收入、房价、成绩等各种数据的分析中，中位数都可以代表一组数据中的典型值。

中位数怎么求、什么是中位数

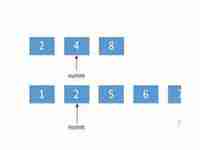
中位数是一组数中居于中间位置的数，即将这组数按照大小顺序排列后，位于中间位置的数。求中位数的方法很简单：将一组数按大小顺序排列后，如果这组数的个数为奇数，那么中位数就是这组数中间位置的那个数；如果这组数的个数为偶数，那么中位数就是中间两个数的平均数。例如，对于一组数：2, 3, 5, 7, 8，其有5个数，所以中位数是5。而对于一组数：1, 2, 4, 5, 8, 9，中间的两个数是4和5，因此中位数是（4+5）/2 = 4.5。

什么是中位数

中位数是一组数据中，按照大小排列后处于中间位置的数值。如果数据的个数是奇数，那么中位数就是这组数据中最中间的那个数；如果数据的个数是偶数，那么中位数就是中间两个数的平均数。中位数的概念常用于描述一组数据的“中心位置”，它具有较好的代表性，不受极端值的影响。

中位数是什么

中位数是一组数中排在中间的数，或者是中间两个数的平均值。中位数通常用来表示一组数据的中心位置，与平均数一样，可以反映出一组数据的集中趋势，但对于数据中有极端值、或者数据不服从正态分布的情况，中位数会更加稳健。在统计学和数据分析中，常常使用中位数来代表一组数据的集中趋势。

中位数的概念及公式

中位数是一组数中的中间值，即把数值按照大小排列，位于正中间的那个数。如果数值的个数是奇数，中位数就是排序后正中间的那个数；如果数值的个数是偶数，中位数就是排序后中间两个数的平均值。中位数的公式如下：。1. 数组元素个数为奇数：中位数 = 排序后位于中间的数。2. 数组元素个数为偶数：中位数 = 排序后中间两个数的平均值。例如，有以下一组数：2, 3, 6, 8, 10。这组数的中位数是6。又例如，有以下一组数：2, 3, 6, 8, 10, 12。这组数的中位数是$(6+8)/2=7$。